Tasub end soojalt riidesse panna, välja minna, leida mugav vaatlusplats, tass ja termos sooja teega kättesaadavaks muuta ning loota, et eriti just 13/14. detsembri öö on selge. Aasta viimasel kuul vaatab taevasse astronoom Alar Puss.
Päike talvepesas
Alanud on detsember, kõige pimedam kuu aastas. Päike paistab madalas silmapiiri kohal orienteeruvalt vaid 6 tundi. Kuna lühikest aega näha olev Päike paistab madalalt, soojendavad päikesekiired maapinda ja õhku selle kohal suhteliselt vähe. See aga toob omakorda kaasa asjaolu, et isegi keset päeva selgeks minev taevas ei too kaasa ilma soojenemist, pigem hoopis vastupidi. Detsembris ja jaanuaris pole haruldane ka olukord, kus pilvise öö sula järel kattuvad päeval lombid jääga, kuna ilm läks hommikul selgeks…
Nii võib juhtuda ka veebruaris, kuid siis on olukord erandlikum: kaasnema peab intensiivne külma õhu juurdevool.
Päike on kuu algupoolel Maokandja tähtkujus, 18- ndal siirdub Amburi tähtkujju. Amburi tähtkuju on aga Päikese jaoks talvepesa, sest 21. detsembril kell 17.03 on talvise pööripäeva moment, kui Päike saavutab oma lõunapoolseima asendi taevaekvaaatorist. Päev on sel kuupäeval aasta lühim ja järgnev öö omakorda aasta pikim. Samuti on Päike 21. detsembri keskpäeval kõige madalamas asendis taevas.
Kuigi suurt vahet pole terve kuu vältel: Päike on ju iga päev madalas ning päev lühike.
Planeedid detsembrikuu öös
Kõige paremini on tänavustel detsembriöödel nähtav Jupiter. Jupiter, asudes Kaksikute tähtkujus, tõuseb üha varem ja on vaadeldav suurema osa ööst (hommikupoole). Kuu lõpus võib juba öelda, et Jupiter on nähtav heledaima tähena taevas kogu pika detsembriöö vältel; siis asub Jupiter kõrgeimas asendis taevas just kesköö paiku ja hiljemgi.
Jupiteri lähedal, veidi kõrgemal on näha Kaksikute tähtkuju heledaimat päris-tähte nimega Polluks.15-ndal on Jupiter möödumas Polluksist; planeet asub tähest 6.5 kraadi lõuna pool (allpool). Omakorda Polluksist kõrgemal asub teine Kaksikute suhteliselt hele täht, Kastor.
Võib seega öelda, et suhteliselt sarnaselt eelmise aastaga paistab „planeetide kuningas" Jupiter taevas uhke Jõulutähena. Jõulutähti seega taevas jätkub, sest vanade eestlaste Päris-Jõulutäht, ametliku nimetusega Kapella Veomehe tähtkujust, tõuseb suurte pühade aegu samuti keskööks kõrgele lõunakaarde, veelgi kõrgemale kui Jupiter. „Kompensatsioooniks" on Kapella omakorda mitte nii hele kui Jupiter.
7-ndal detsembril vastu 8-ndat on Jupiteri lähedal Kuu.
Kuu asub siis Jupiterist vasakul, ning otse allpool Polluksist; veel kõrgemal asub ju Kastor. Kokku moodustub midagi L-tähe taolist. Kui vaid Kuu liiga suur ja hele poleks…
Õhtupoole ööd, umbes poole öö vältel, on lõuna-edelataevas, Jupiteriga võrreldes märksa madalamal, näha Saturni. Planeet asub Veevalaja tähtkujus ja on võrdluse mõttes umbes sama hele kui Jupiteri lähistel paiknev Polluks Kaksikute tähtkujust.
26-nda detsembri õhtul, päev enne esimese veerandi faasi on Saturnile lähimas asendis Kuu.
Kuu alguses on planeete näha ka madalas hommikuses koidutaevas.
Veenus on kuu esimesel dekaadil nähtav kehvades tingimustes väga madalas kaugutaevas. Planeet tõuseb juba kuu alguses veidi vähem kui tund enne Päikest, vaatlusaeg lüheneb ka edaspidi ning teise dekaadi alates kaob Veenus koiduvalgusse. Veenus jõuab siiski enne koiduvalgusse kadumist tähtkujudes rännata, liikudes Kaaludest läbi Skorpioni Maokandja tähtkujju.
Kuuga Veenus neil nähtavuse hommikuil ei kohtu.
Veenusest paremini peaks sedapuhku näha olema Merkuuri. Merkuur on muidugi iseenesest alati Veenusest tuhmim, kuid vaatlustingimused on seekord paremad. Merkuur peaks kuu keskpaigani olema leitav hommikuti kagutaevas, tõustes veidi üle 2 tunni enne Päikest. Ka Merkuur liigub Kaalude tähtkujust läbi Skorpioni Maokandjasse. 18-nda paiku kaob Merkuur koiduvalgusse.
Ka Kuu ja Merkuuri lähikohtumist sedapuhku ei toimu.
Seega pühade ajal peame leppima vaid Jupiteri ja Saturniga. See-eest paistab hele Jupiter aga väga hästi, suisa terve öö. Teleskoobis on mõlemad planeedid aga väga muljetavaldavad. Jupiter oma 4 kaaslasega meenutab teleskoobivaates ju suisa miniatuurset Päikessüsteemi.
Lugupeetud lugeja võib kahtlustada, et vahest on planeet Marsi nähtavus juba mitmete kuude vältel ununenud kirja panna. Kuid mida sa ikka kirja paned, kui pole suurt kirja panna. Tänavuse aasta teises pooles paraku Marss nähtav olnud ei ole, erandiks pole ka detsember ning etteruttavalt võib öelda, et ka näärivana, kes peaks ju aastavahetuse tulekut kuulutama, Marssi kaasa ei too. Mis siiski muidugi ei tähenda, et Marss kogu uuel aastal paistmata jääks!
Muuseas, miks kipub alailma ja läbi aegade olema mingi probleem seoses jõuluvana ja näärivanaga: kord ei tohtivat olla ja seega ka tulla üht, kord teist! Aga mis saab kingihuvilistel selle vastu olla, et nädalase vahega tuleb kokku suisa kaks, ehkki välimuselt väga sarnast, kingikottidega „vana"?! Aga nojah, saagem aru ja samuti saagem ometi hakkama: aega on ju mõlemal tegusal habemikul alati vähe; kord on ühel vaja Ukrainat taaskord „taas-lehtmestada", teisel jälle arvukatel maski- ja süstilaatadel osaleda… Iga tubli ajupestud pioneer meie hulgast saabki aru ja ütleb ka nagu nõutud: „Saame hakkama!"
Kuu faasid detsembris on järgnevatel ajamomentidel.
Täiskuu 5-ndal kell 1.14, viimane veerand 11-ndal kell 22.52, noorkuu 20-ndal kell 3.43, esimene veerand 27-ndal kell 21.10.
4. detsembri hommikul asub peaaegu täis Kuu Taevasõela ehk Plejaadide tähteparve taustal, 31. detsembril õhtul (faas on jälle paraku suur) aga Plejaadide kõrval.
Ööd on pikad…
Detsembriöö on pikk ja kui ikka ilm lubab, on vaatamist palju. Ei teagi kohe, mida esile tuua. Noh, näiteks ehk kuu alguses peale keskööd, kuu lõpus aga kesköö paiku üle pea põhjast lõunasse kulgevat Linnuteed. Kuu alguses on ka varaõhtuti veel Linnutee kõrgel, kuid see on meie suure täheketta teine haru ehk siis osa.
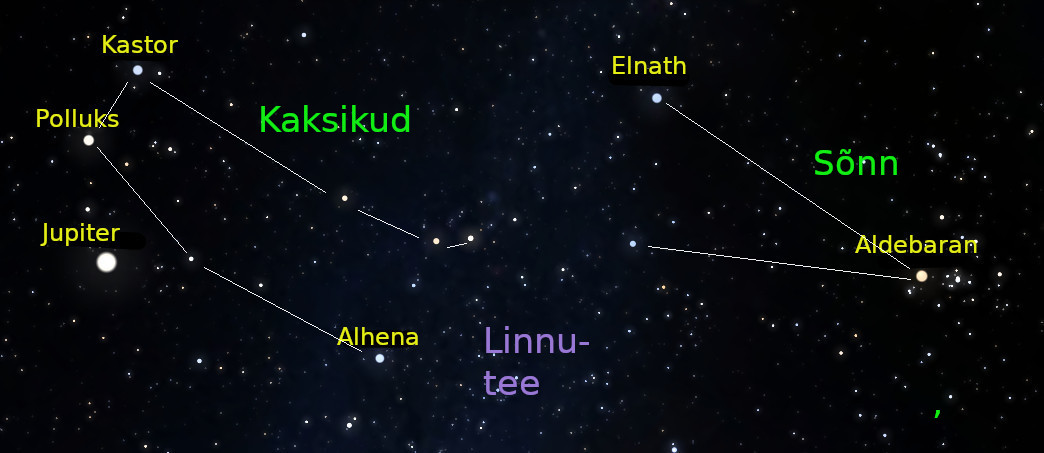
Pikk detsembriöö näitab meile ära kõik Eestis nähtavad esimese suurusjärgu ehk siis heledamad „päris-tähed" peale Antaarese.
Detsembriõhtune madalam lõunataevas ja Fomalhaut
Novembrikuus sai tutvustatud hilissügise hilisõhtute lõunakaare kõrgemaid tähtkujusid, neis sisalduvaid galaktikaid (ning „igaks juhuks" ka „ronimisharjutusi nende galaktikate juurde").
Veidi võiks nüüd pilgu heita ka Andromeedast ja Pegasusest suuna mõttes madalamal paiknevatele tähtkujudele, sest võib-olla muidu seda keegi eriti teha ei viitsitaks. Kuigi, jah, detsembrikuu kulgedes „kuivab" selle taeva-ala nähtavusaeg lõunakaares üha varasematele õhtutundidele.
Veevalaja, Kalad, Vaal… Puha veega seonduv. Kuna need tähtkujud ei sisalda ka silmatorkavaid iludusi ehk siis heledaid tähti (Saturn on praegu meeldiv, kuid ajutine erand), siis ongi see ala kuidagi „vesise taevaalana" tuntud. Siiski võiks astronoomiahuviline teada nendegi tähtkujude olemaolust. Ning küllap leiab siitki edasi lugedes ka tõendeid, et allakirjutanu siiski ei taha austatud lugejaid lihtsalt „tühjas ruumis ekslema" juhtida.
Piirkonna heledaim „päris-täht" on teise tähesuuruse (täpsemalt 2.04 tähesuurust) täht Deeneb Kaitos Vaala tähtkujust. Mitte just eriti hele, aga kuna muud ümbruskonna tähed on veel tuhmimad, pole seda tähte raske üles leida.
Deeneb Kaitos (tõlkes Vaala Saba) asub meist umbes 96 valgusaasta kaugusel. Selline kaugus pole küll ülisuur, kuid siiski ei saa siinsel juhtumil rääkida Päikesele (ja Maale) suhteliselt lähedasest tähest.
Paneme tähele, et Vaala tähtkuju kontuur on praegu selline, et saba asub ida pool (vasakul). Siit võiks püstitada omapärase küsimuse: kas Vaal on tähtkujuna kunagi minevikus paiknenud teistpidi ja nüüdseks end ümber pööranud? Kui, siis millal ja KUIDAS see toimus?
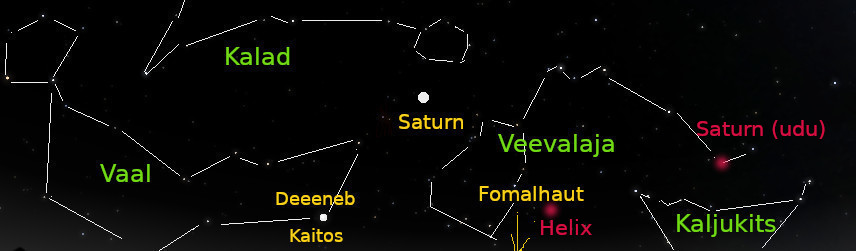
Vaalast kõrgemal paikneb Kalade tähtkuju. Üsna ühtlaselt tuhmide tähtede kaks rida, mis kohtuvad omavahel teravnurga all. Kumbki rida lõpeb kujuteldava kalaga. Teritades veidi ka kujutlusvõimet, on nii ülemine (nn Põhjakala kui parempoolne (nn Läänekala) lapiku, ilmselt siis „lestakala" moodi.
Samasuguse „lestakalana", sabauime asemel, võib ette kujutada ka Vaala tähtkuju parempoolset ülemist osa. Nojah, maitse asi, muidugi. Kuid kellele see vaala sabauim ikka eriti maitseb…
Vähemalt esmapilgul veel viletsama mulje kui Kalad ja Vaal jätab endast Veevalaja tähtkuju. See paikneb eelmistest paremal pool ehk lääne pool. Hoolikas uurimine võiks ehk viia järeldusele, et tegu on viltuse ümberpööratud veeanumaga, mille pikk ja halvasti kokkuvaadeldav „käepide" kulgeb mitmes sik-sakis paremale poole, ulatudes äärmises parempoolses osas täpselt Kaljukitse tähtkuju kontuuri keskosa kohale.
Kaljukits paikneb suheliselt laia tähtkujuna edelataevas üsna madalas; alumine osa asub üsnagi silmapiiri lähedal.
Kontuur on siingi huvitav, meenutades justkui veevanni, mille põhi on miskipärast mitte tasase, vaid nürinurkse kujuga: põhja „tipuserv" jääb „vanni" keskele. Kuidas küll selline „vann" „otse püsib"?
Kuu teises pooles kipub Kaljukits üha enam ehavalgusse kaduma.
Õhtul kella 18 ümbruses, kuu teisel poolel aga pigem millalgi peale kella 17, kui parajasti on pimedus süvenenud, tasub leida vaba vaate lõunapoolse silmapiirini. Piirkond silmapiiri lähedal taevas, mida taga ajame, jääb Veevalaja „hädisest" põhikontuurist allapoole ja veidi paremale.
Kuna harvesterid üha möllavad ja metsi aina rüüstatakse, siis polegi ehk eriti raske meetrikõrguste kändude vahelt sobivat suunda leida. Lõuna-Eestis umbes 2 ja poole kraadi, Põhja-Eestis aga veidi alla 2 kraadi kõrgusel, vaatab pilvede puudumisel vastu üksik küllatki hele täht. Võrdluseks: täiskuu läbimõõt on pool kraadi, nii et täht on täitsa vaadeldav. Kui vaid neid pilvi ees ei ole ja loodame, et neid mõnel õhtul ikka pole!
Tegu on esimese suurusjärgu tähtede ühe esindajaga, nimetuseks Fomalhaut. Täht asub Lõunakala tähtkujus (veel üks kala juures!), mida üldiselt loetakse Eestis mitte vaadeldavaks. Ning üldiselt tahetakse lugeda Fomalhauti lõunataeva täheks; ikka just selles mõttes, et tähte Eestis ei näegi. Aga ometi ju näeb, kuigi harva ja kehvades tingimustes; vaadake teie ka!
Fomalhaut (1.17 tähesuurust) oli ja on ka järgmistel aastatel (kuigi 1 öö mastaabis samuti suhteliselt lühiajaliselt) lisaks detsembriõhtutele nähtav ka sügiskuudel.
Ometi peab ütlema, et Põhja-Eestis paistab Fomalhaut siiski halvemini, sest paksu atmosfääri efekt halvendab nähtavust silmapiiri lähedal juba vähem kui kraadi jagu „veel allpoole" vaadates.
Saturn ja Helix
Veevalaja tähtkujus asub praegu kaks Saturni.
Jajah, lugesite õigesti: Saturne on kosmoses kokku kaks ja praegu on mõlemad suisa samas tähtkujus!
Saturnid asuvad „igaks juhuks" siiski tähtkuju eri äärtes. Kalade tähtkuju poolses Veevalaja ääres „istub" heleda tähena planeet Saturn, parajasti heleduselt üsna võrdne lisaks Kaksikute Polluksile ka Fomalhaudiga. Et Fomalhaut vist siiski tuhmim tundub, see tuleneb paksemast atmosfäärikihist vaatesuunal.
Veevalaja selles osas, mis „venib" Kaljukitse tähtkuju kohale, asub aga teine Saturn! Miinuseks on paraku see, et seda pole kahjuks palja silmaga näha. Tegemist on ühega kosmilistest udukogudest, mis on alaliigina tuntud planetaarsete udukogudena.
Tuntuim katalooginimetus on „sellel" Saturnil järgmine:
NGC 7009.
Saturn on visuaalselt üldjuhul teleskoobis nähtav „tähest ulatuslikuma tähena", mis ühes tasandis on rohkem välja venitatud.

Süvateava objektide silmaga nägemiseks on tänapäeval mõnelgi juhul suhteliselt lihtne kasutada mingit kuskilt ostetud „tarka teleskoopi", mida saab kergesti kaasasoleva tarkvara menüü järgi juhtida. (Kui vaid teleskoop ikka õigesti paika on sätitud ning just see võib olla keeruline!)
Veevalajaga seoses võiks veel ühest planetaarudust rääkida. Selle nimetus on Helix, katalooginumbriga NGC 7293. Ilupilte sellest on palju; piltide sarnasus kuulsa Lüüra uduga on märkimiseväärne. (Saturnist (neist mõlemaist) on muidugi ka ilupilte.)
Kuid teleskoobiga reaalne Helix-i vaatlemine on keeruline ning vajab igatsugu katsetamist ja proovimist; võib kergesti juhtuda, et udukogu jääbki nägemata. Asi on selles, et Helix (põhikujult rõngas) on suurim planetaarudu Maalt vaadates. Omakorda selle põhjus on objekti suhteline lähedus: udukogude kohta on Helix-i kaugus tõesti „napp", „vaid" 700 valgusaasta kanti.
Väikese teleskoobi võimekus (telekoobi läbimõõt, valitud suurendus) võib liialt vähene olla. Teisalt, suurema teleskoobi ja suurema suurendusega võime lihtsalt udurõnga keskel oleva suhtelise tühjuse suunas vaadata…

Asja teeb Helix'i juhul keerulisemaks ka paksema Maa atmosfääri probleem seoses udukogu suhteliselt madal asendiga taevas. Kuid teleskoobipargi ja okuaaride heal valikul ning entusiasmi olemasolul võib proovida Helix-iga „mängida"…
Teleskoopide kasutamise kohta üldiselt teeme lähemalt juttu allpool.
Geminiidid
Detsembris on põhjust rääkida ka meteoorivooludest. Sedapuhku on vähemalt üks neist täitsa „asjalik", nimetusega geminiidid.
Meteoorivoole on aasta jooksul päris mitmeid. Kuid „kõige korralikumaid" ja seda suisa iga-aastaselt, on vaid 3 tükki. Uhketest augustikuistest meteooridest oli suvel juttu, nüüd on järg geminiidide käes.
Nagu nimetus reedab, on radiant ehk näiv meteooride saabumissuund Kaksikute tähtkujus. Ning see tähtkuju tõuseb detsembris just kesköötundideks kõrgeimasse asendisse lõunataevas. Tänavu siis koos eriti heleda „tähe", Jupiteriga.
Radiandi kõrgus mõjutab (ühena tingimustest) lendtähtede esinemissagedust. Uurivalt taevasse vaadata võib aga ükskõik millises suunas! Kui meteoore leiab ühest suunast (nt itta vaadates), siis esineb neid ka muudes suunades (nt lääne suunas vaadates), kuigi enamasti mitte muidugi samaaegselt.
Geminiidid esinevad hinnaguliselt umbes 4-st 17-nda detsembrini.
On olemas ka „laiemaid hinnaguid", nt koguni 19. novembrist 24. detsembrini.
Geminiidde tippaeg peaks saabuma 13-nda detsembri ööl vastu 14-ndat. Nii et analoogia augustikuiste lendtähtedega on ka kuupäevade mõttes täiesti olemas!
Geminiidid kui suur hulk meteoorosakesi on kuidagimoodi „välja löödud" mitte komeedist, vaid asteoridist, nimetusega 3200 Phaethon.
Asteroidid üldiselt ei liigu oma orbiitidel nii kiiresti kui komeedid. Nii ka antud juhul.
Sellest tuleneb, et ka 3200 Phaethoniga seotud geminiidiide meteoorid ei kihuta Maa atmosfääri niivõrd suure hooga nagu nt perseiidid augustis. Geminiidide keskmine kiirus Maa atmosfääri sisenemisel on „vaid" 35 km/s. (Seevastu perseiidide puhul on see kiirus 60 km/s ümbruses!) Seetõttu võib mingi konkreetse geminiidi lendu (mitte küll igal juhtumil) jälgida suhteliselt pikka aega. Kui langevad meteoorid satuvad olema heledad ja tihti nad geminiidide puhul seda ka on, siis võib vahel jätkuda aega „erutavate mõtete" tekkimiseks: ega see ometi viimati alla kuku?
Geminiidide meteooride keskmine tunniarv (nagu ka augusti-meteooridel) on 100 – 120 või enamgi. Nii et tasub küll end soojalt riidesse panna, välja minna, leida mugav vaatlusplats võimalusega kuskil istuda, tass ja termos sooja teega kättesaadavaks muuta ning loota, et eriti just 13/14. detsembri öö on selge.
Kuidas on lugu Kuuga? See ju segab meteooride vaatlemist. Lugu on sedapuhku mitte just halb. Kuu on „vana", faas on veidi üle viimase veerandi, Kuu tõuseb peale keskööd ja ei tõuse ka hirmus kõrgele. Kesköötundide aegu on aga radiant maksimumkõrgusel; „maksimaalse maksimumi" aega eeldatakse kella 2 ümbruse kanti; siis veel Kuud taevas ei ole. Nii et geminiidid on sedapuhku päris hea nähtavusega.
Kuidas siis ikka geminiidide osakesed asteroidist tekkinud on? Tõenäoliseim põhjus on selles, et 3200 Phaethon sobib oma orbiidi poolest küll asteroidiga, kuid on oma olemuselt hoopis „uinunud" komeet, millest praegu silmanähtavalt materjali ei pudene. Tasub seda objekti edasi uurida!
Ursiidid
Teine detsembrikuu meteroorivool on ursiidid, radiandiga Väikeses Vankris. See asjaolu teeb ursiididest vaid poolel maakeral (mõistagi põhjapoolkeral) nähtava meteoorivoo. Mis on omakorda üks oluline asjaolu, et ursiide nimetatakse juba kaua aega väheuuritud meteoorivooks, kuigi uuringute hulk siinselgi juhtumil ajas üha kasvab.
Ursiidid on jälgitavad 17-ndast 26-nda detsembrini. Kuna maksimum satub 22. detsembrile, võib ursiide nimetada ka talvise pööripäeva meteoorideks. Eeldatav intensiivsus on geminiidest madalam, kuid mõnikord on esinenud ootamatuid positiivseid üllatusi ka ursiidide puhul.
Parim vaatlusaeg peaks seekord olema 22. detsembri varahommikul enne valgenemist.
Aga Kuu? Ei, Kuu ei sega üldse; alles 20-ndal detsembril oli kuuloomine!
Eelteade
Kohe uue aasta alguses lisandub veel iga-aastane kolmas võimas meteoorivool, kvadrantiidid, maksimumiga 3. jaanuari ööl vastu 4-ndat. See meteoorisadu on sama tihe või ehk tihedamgi kui perseiidid ja geminiidid, kuid tihe meteooride „väljalöögi periood" on vaid mõnede tundide pikkune; see võiks sedapuhku mainitud ööl olla enne keskööd.
Kuid… „Oh kui paha, ma ei taha, laske siin ma lähen maha!…" Sest just 3. jaanuaril on sedapuhku ju ka täiskuu!
Optikaseadmetest
Astronoomiliste vaatluste juures on sageli oluline teleskoobi olemasolu; teaduslike uurimuste puhul on see suisa möödapääsmatu. Ka Astronoominurga juttudes on päris tihti teleskoopi mainitud. Mida aga kujutab endast teleskoop?
Enne teleskoopi peaks veidi tutvuma lihtsaimate optikaseadmetega: läätsedega.
Küllap on enamus inimesi kui mitte luupi kasutanud, siis kuulnud sellest vast ikka. Lihtsaim luup kujutab endast üht põhilist läätsetüüüpi, nimelt kumerläätse.
Läätsede tüübid
Kumerlääts on olemuselt tükike suure läbipaistvusega osavalt siledaks lihvitud klaasi. Erinevus näiteks ümmarguse aknaklaasiga on see, et läätse mõlemad küljed on kumerad: paksus on läätse keskel suurem kui läätse äärtel.
Mõlemast küljest kumer lääts ehk kaksikkumer lääts pole siiski ainuke läätse variant. Läätse vastaskülgede kumerus võib olla erinev; üks külgedest võib ka tasane olla. Siis on tegu tasakumera läätsega.
Teine läätse põhivariant on nõguslääts. Sellisel juhul on lääts keskelt õhem kui külgedelt. Selline lääts luubiks kindlasti ei sobi.
Ka nõgusläätse küljed ei pruugi olla võrdväärse kujuga. Näiteks võib ka nõgusläätse juhul esineda variant, kui teine läätse külg on tasane. Selline lääts on tasanõgus.
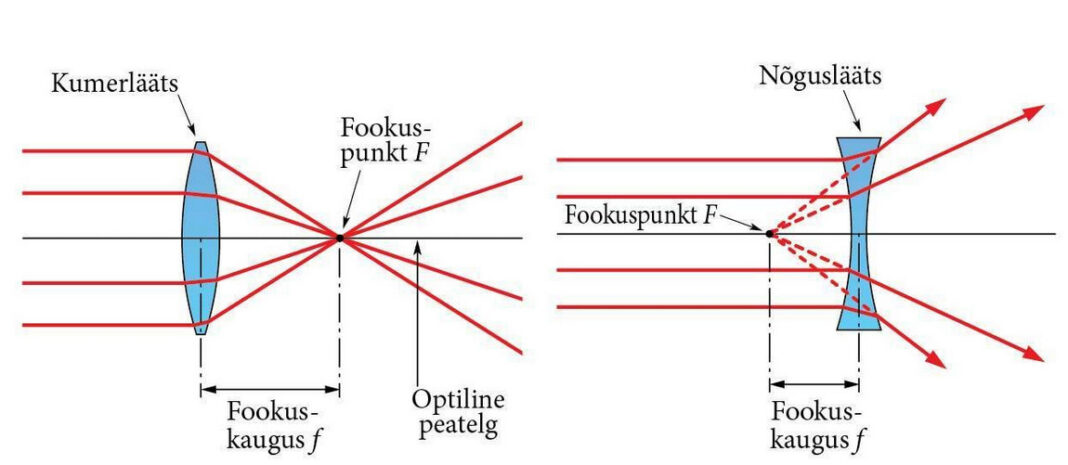
Esinevad ka sellised variandid, kus läätse üks külg on kumer, teine aga nõgus. Olenevalt sellest, kumb kõverus on suurem, nimetakse sellist läätse kas positiivseks meniskiks või negatiivseks meniskiks. Esimesel juhul on suurem läätse kumera külje kõverus, teisel juhul on suurem nõgusa külje kõverus.
Sellseid läätsi nimetatakse ka vastavalt nõguskumerateks (kokkuvõttes pigem kumer lääts) ja kumernõgusateks (kokkuvõttes pigem nõgus lääts).
Kui lääts on üleni „liialt"paks, on läätse omaduste matemaatiline kirjeldamine keerukam kui õhukese läätse juhul.
Siiski sobib paljudel juhtudel, nii kumerläätsede kui nõgusläätsede puhul, õhukese läätse lähendus. Sellisid läätsi peaks kirjeldatama esimest korda juba põhikoolis. Kui muidugi „sooideloogiast" ja muudest hullustest aega üle jääb ning tundub, et üha vähem seda aega jääb. Kusjuures hirmuäratavalt paljude pedagoogide kindlate väärveendumuste taustal!
Läätsedele on omane fookuskauguste mõiste. On olemas nii läätse eesmine kui tagumine fookus (vastavalt valguse leviku suunale). Kui lääts on „tavaline" ehk (mõlemast küljest võrdselt) kaksikkumer või kaksiknõgus, siis on nii eesmine kui tagumine fookuskaugus, lähtuvalt läätse keskpunktist, võrdsed.
Fookused asuvad läätse optilisel teljel. Optiline telg on omakorda sirge, mis läbib läätse keskpunkti ja on sihilt risti läätse diameetriga (ehk siis on läätse klaaskeha keskelt läbiva tasapinnaga) risti.
Fookus tähendab läätse puhul seda, et kumerläätsele langev paralleene kiirtekimp koondub pärast läätse läbimist läätse tagumisse fookusesse kokku. See tähendab, et praktiliselt ühte punkti koondub kogu läätsele langev paralleelne valguskiirte kimp. Fookuse punkti koguneb ka palju üldist kiirgusenergiat ja temperatuur tõuseb seal kiiresti.
„Katse-eksituse" meetodil on sel põhimõttel vahel nt koolipoisid kasutanud luupi Päikese kiirte abil mingite pindade põletuste ja suitsu tekitamiseks. Mõistagi on selline tegevus ohtlik, sest sellest võib areneda ka kontrolli alt väljuv tulekahju.
Aga katsu sa õpilast milleski keelata! Kohe oled ise trellide taga ja uurimisel! Seda „vabakasvatuse" jama hakati arendama juba kuskil 30 aasta eest. Õnnetud õpetajad… Ning muidugi ka õnnetu, nüüdseks juba ise ka 30 kuni 40 aastat vanaks saanud põlvkond (ja nooremad ka), kes ise on juba väärideoloogia „viljakates tingmustes" üles kasvanud. Rääkimata omakorda nende järeltulijatest… Homo Europicus, mida muud. Mida ongi ju tahetud teha!
Üks kumerläätsede olulisi rakendusi ongi juba eespool mainitud luup, liialt väikese kirja lugemiseks väga kasulik.
Teleskoop – esimene katse
Nüüd oleme jõudnud tavalistelt karjamaadelt astronoomide marjamaale! Sest jutt on teleskoopidest!
Kõigepealt võiks õhku visata provotseeriva küsimuse. Planeedid ja tähed eriti on ju tohutu suured; mis suurendust teile veel vaja on?
„Infotunni „miihal-vastus": „On selgesti näha, isegi läbi minu valelike prillide, et te esindate oma küsimusega Kremli huve ja räägite Putini jutupunkte! Kuutin on lunn!"
„Juhataja, see vastus ei rahulda. Kutsuge vastaja korrale."
„Vastaja „ see lugupeetud härra"*, püsis teemas. Ma ei saa sekkuda. Küll aga tahan teile endale öelda, et ma ei salli selliste putinistlike küsimuste esitamist ja mis siis et ma räägin sageli teie küsimustele vahele, ei anna ma teile lisaaega, kuna see kõik on minu enesekorralduslik asi ja… kuulge… kus ma olen ja miks ma olen ja kes ma olen?" (Ronib laua alla ja hakkab algaja hundi kombel ulguma; üha enam lisandub ka „röh-röh"-e.)
* – jutumärgid on lisatud autori poolt.
Kõik on tegelikult loogiline, sest igaühel olla ju õigus end igal suvalisel hetkel pidada mistahes olendiks iganes ja lisaks nõuda ka teistelt nende valikute tunnustamist…
Katsume siiski kuidagi teema juurde tagasi minna. Tundub, et vastus polnud siiski õige. Kuid jätame küsimuse meelde.
Teleskoop – uus katse
Teleskoopi kasutatakse (erinevalt mikroskoobist) mitte lähedal paiknevate, vaid kaugete esmete vaatlemiseks.
Kauged esmed paistavad aga ju kaugelt eemalt märksa väiksemad kui nad tegelikult on. Öötaeva kauged objektid, planeedid ja tähed, paistavad ju paljale silmale lausa punktikujulised. Nii et põhjust täitsa on objektide nähtavust parandada või siis teisiti öeldes vaatenurka objektile suurendada. Mis siis, et need kauged objektid iseenesest niigi suured on.
See ongi vastuseks eelmises punktis püstitatud küsimusele.
Teleskoobi põhiidee on süsteem kahest läätsest. Neid läätsi nimetatakse objektiiviks ja okulaariks. Mõlemad läätsed on kumerläätsed (siiski võib teleskoobi okulaariks olla ka nõguslääts, kuid seda varianti üldselt eriti ei kasutata).
Teleskoobi korral on väga oluline objektiiviks oleva läätse diameeter ehk läbimõõt: mida suurem see on, seda uhkem.
NB! Peaks ehk üle kordama, et läätse läbimõõdu ehk diameetri all peame silmas ikka alati selle mõõtmist mingis sihis, mis on ristisuunas läätse optilise teljega! Piki optilist telge mõõdetavat läätse linaarmõõdet nimetatakse ju hoopis läätse paksuseks ning see on palju väiksem kui läätse diameeter. Läätse paksus „ümardatakse" praktikas väga kasulike õhukese läätse valemite tuletamisel suisa olematuks!
Tagasi teleskoopide juurde. Väiksema diameetri ehk läbimõõduga läätseks on teleskoobis okulaar; ka on okulaari fookuskaugus objektiivi fookuskaugusest märksa väiksem.
Teleskoobi sees peavad objektiivi okulaaripoolne fookus ja okulaari objektiivipoolne fookus asuma ühes ja samas kohas!
Suurendus
Sageli on esimeseks küsimuseks: palju see teleskoop suurendab?
Teleskoobi puhul määrab suurenduse just objektiivi ja okulaari fookuskauguste suhe ehk jagatis: M = Fobj / Fokul.
Tähised on sellised.
M – suurendus;
Fobj – objektiivi fookuskaugus;
Fokul – okulaari fookuskaugus.
Teleskoobi suurendust on võimalik esitada ka objektiivi läbimõõdu ja väljundava suhtega:
M = Dobj / Dväljund.
Tuleb panna tähele, et väljundava Dväljund ei tohi automaatselt samastada okulaarläätse läbimõõduga Dokul. Üldjuhul on Dväljund väiksem kui Dokul. (Kuigi hea õnne korral võib siiski ka nende „D-de" segiajamise korral enam-vähem õige tulemuse saada. Kuid kes see ikka kasiinos kaarte mängida tahab…) Neist läbimõõtudest teeks uuesti lähemalt jutt allpool.
Võimalikke okulaare on aga enamikel teleskoopidel mitmeid.
Asi on selles, et okulaare saab üldiselt suhteliselt kerge vaevaga vahetada (seevastu teleskoobi objektiivi väljavahetamine tähendaks teleskoobi lammutamist ja uue ehitamist).
Seega on teleskoobi suurendus muudetav suurus.
Okulaarid tehakse üldiselt päris väikesed, okulaari ja ühtlasi kogu teleskoobi väljundava (kordaks üle: see ei võrdu okulaari läbimõõduga!) ja fookuskaugust väljendatakse enamasti millimeetris: fookuskauguse suurusjärk on okulaaridel mõni cm ehk mõnikümmend mm, väljundava läbimõõt on kasulik isegi veel väiksem saada kui 10 mm (ehk siis alla 1 cm).
Niimoodi, okulaare koos nende fookuskaugustega „väiksemaks" vahetades, võib saada teleskoobi arvuliselt suuri suurenduse numbreid miks mitte suisa tuhande kanti. Seda isegi juba suhteliselt väikese (ehk siis suhteliselt väikese objektiivi läbimõõduga, kuigi suhteliselt pika fookuskaugusega teleskoobi abil)! Kuid edasi lugedes peaks selgeks saama, et selliselt saadud „giga-mega-suurendus" on üsna mõttetu.
Ülearu suurt suurendust „taga ajada" pole mõtet isegi suurte teleskoopidega. Kasuliku ehk mõtteka, detaile lahutava suurenduse ülempiir oleneb teleskoobi suurusest ehk objektiivi läbimõõdust. Tõsine lisaprobleem on aga siin see, et Maa atmosfäär paneb teatud piiridest alates, mis seejuuures on muutlikud, „käe vahele". Selle probleemi juurde tuleme kohe tagasi.
Vaatame uuesti eespool kirjutatud suurenduse valemit. Suurema suurenduse jaoks peaks niisiis objektiivi fookuskaugus olema võimalikult suur ja okulaari puhul peaks fookuskaugus olema omakorda võimalikult väike.
Sellepärast peaks ju ka teleskoobi toru üsnagi pikk olema; toru pikkuse praktiliselt määrabki ju objektiivi fookuskaugus.
Seetõttu püüti ajaloolises mõttes kunagi ehitada ka ülimalt pikkade torudega teleskoope.

Optikatööstuse edenedes said aga võimalikuks üsnagi väikesed okulaarid väikeste fookuskaugustega; sellised ongi ju kaasajal kasutusel. Kuna selliseid okulaare tehakse, siis on sama suurenduse saamiseks asi ju palju lihtsam. Pole enam vaja ehitada teleskoopi hiiglaslikult pikaks, seda siis objektiivläätse võimalikult suure fookuskauguse tarbeks.
Kui jätta mängust välja maakera atmosfäär, mille mõju enamikel juhtudel juba märksa väiksemaid suurendusi saada püüdes segama hakkab, siis teleskoobi maksimaalne kasulik suurendus on eri hinnagutel umbes selline: 1 kuni 1,5 korda teleskoobi objektiivi läbimõõt millimeetrites. On ka veidi suuremaid suurenduse ülempiiri hinnanguid (2 kuni 2,4 kordne objektiivi fookuskaugus millimeetrites) kuid need tunduvad pigem liiga optimistlikena.
Hinnangu hajuvuse põhjus tuleneb praktikast, erinevate konkreetsete objektide, näiteks lähestikku paistvate kaksiktähtede vaatlustingimustest: heledamate ja tuhmimate tähtedega juhtudel on piirid veidi erinevad.
Kui kaksiktähe komponendid on heledad, võib kasutada suurimaks suurenduseks pigem seda „1,5 korda… varianti. Tuhmimatel juhtudel tundub aga just see suurendus, mis võrdub täpselt teleskoobi fookuskaugusega millimeetrites, omakorda „õigem" olevat. Katsetamisel võib muidugi tekkida vajadus „õige" arvulise hinnagu andmiseks kasutada ka mingit muud arvu 1 ja 1.5 vahel, millega objektiivi millimeetrites antud läbimõõt läbi korrutada.
Taevakehade „võimalikult hea" suurenduse probleemile detailsemalt lähenedes tuleb esile muidki keerulisemaks tegevaid asjaolusid, aga selleks pikaks kursuseks ei jää ju siinkohal aega.
Suurendus on alati ühikuta suurus.
Kuid suurendus polegi tegelikult teleskoobi ainus oluline parameeter.
Lahutusvõime
Teleskoobi oluline parameeter on ka lahutusvõime. See oleneb just objektiivläätse läbimõõdust, okulaari olemus lahutusvõimet ei muuda.
Mida suurem on objektiivi läbimõõt, seda suurem on ka teleskoobi lahutusvõime ehk võime uuritaval objektil detaile eristada. See asjaolu omakorda mõjutab teleskoobi maksimaalset kasulikku suurendust. Ehk siis: suurema teleskoobi (teleskoobi suurema objektiivi läbimõõdu) korral saame suurendust kasvatades (okulaare üha väiksema fookuskaugusega okulaaride vastu vahetades) ka üha suurema detailide eristamise ning nende detailide nägemise võimaluse.
Nagu juba suurendusest rääkides veidi juttu oli, paneb üldiselt esimesena omad piirid ette Maa atmosfäär. See ei lase teleskoobi teoreetilisel lahutusvõimel praktikas sama suureks kasvada kui teleskoobi objektiivi suurus võimaldaks. Väiksemate (alla 20 cm läbimõõduga) objektiivide ja „hea atmosfääri" juhul paneb lahutusvõime piirid paika teleskoobi obektiivi läbimõõt, enamikel juhtudel aga siiski atmosfäär.
„Hea atmosfääri" poolt lubatav lahutusvõime on alla 1 kaaresekundi (räägime ju taevakehade puhul nurkkaugustest). Kuid Eesti tingimustes on atmosfääri tõttu üldjuhul tegu 2 kuni 3, hullematel juhtudel isegi 4 ja vahel harva veelgi enamate kaaresekundite suuruste lahutusvõimetega.
Nagu näha, on arvuliselt asi nii, et suurem lahutusvõime annab väiksemad eristatavate nurkkauguste väärtused ja vastupidi.
Mõistagi on asi nii, et mida väiksem on teleskoobi lahutusvõime, seda väiksem on ka maksimaalne kasulik suurendus (ikka detailide kasvava eristamise mõttes).
Isegi atmosfääri puudumisel paneksid teleskoobi lahutusvõimele (ja seega ka maksimaalsele kasulikule suurendusele) piiri ette valguse laineomadused. Mida suurem objektiivi läbimõõt, seda suuremal suurendusel kasulik piir vastu tuleb. (Atmosfääri mõju me seda juttu rääkides ei arvesta.)
Siit siis tuleneb ka maksimaalse suurenduse võrdelisus ojektiivi läbimõõduga, nagu eespool juttu oli.
Kuid Maa atmosfäär on ju alati olemas; seega teatud piirist (olenevalt atmosfääri tingimustest) alates teleskoobi objektiivi suurendamine enam lahutusvõimet ei tõsta.
Teatud määral võib lahutusvõime piirile jõudes teleskoobi okulaare muutes siiski veidi veel suurendust edasi kasvatada, kuigi detaile rohkem ei eristu.
On aga veel üks ja ehk isegi põhiline põhjus ehitada võimalikult suuri (suure objektiivi läbimõõduga) telekoope (vt allpool). Enne veel aga veidi ka vaateväljast.
Vaateväli
Tuleb panna tähele, et mida suurem on teleskoobi suurendus, seda väiksem on vaateväli, mida vaatleja läbi teleskoobi näeb.
(Siin tuleb esile teatud analoogia ajalehe lugemise katsetamisel luubi asemel mikroskoobiga: suurendus on siis juba liialt suur… Mikroskoopide kirjeldus siiski paraku seekordsesse juttu ei mahu, piirdugem nentimisega, et needki aparaadid on tõesti ikka veel olemas, pole veel „ära keelatud"…)
Tahtes aga läbi teleskoobi „midagi" võimalikult suuremana uurida, kaob „vastutasuks" uuritavat (kaksiktähte või planeeti või galaktikat vm…) ümbritseva muu taeva ilu imetlemise võimalus samas vaateväljas.
(Väga) tuhmide taevaobjektide vaatlemisest
Lisaks parema lahutusvõime saamisele on teinegi ja isegi põhiline põhjus ehitada võimalikult suuri teleskoope; teleskoobi suuruse all mõistetakse selleski seoses just objektiivi läbimõõtu.
Mida suurem on teleskoobi objektiiv, seda suurem on ju objektilt vastavõetava kiirtekimbu läbimõõt, mis teleskoopi satub. Mis omakorda tähendab, et seda tuhmimatena paistvaid taevaobjekte (kõnekeeli: nõrgemaid objekte) on võimalik teleskoobi abiga tuvastada ja nende valgust ka teaduslikult uurida.
Mistõttu tõeliselt suured teleskoobid ei ole enam silmaga vaatamise huvi ja hobi paremaks rahuldamiseks mõeldud amatöörteleskoobid, vaid ikka juba astronoomide pärusmaa.
(Loomulikult saab ka paljusid amatöörteleskoope kasutada teaduslikeks vaatlusteks. Seega mingit kindlat piiri amatöörteleskoopide ja „astronoomide tööteleskoopide" vahel mõistagi ei ole.)
Kui mälu ei peta, on ka siinses Astronoomianurgas
ennegi rõhutatud, et termin „amatöör" ei ole „mahategev", vaid ikka kiitev hinnang! Seda tuleb ikka ja jälle korrata ja rõhutada.
Üks hoopis teine asi, mida vahel on vaja siiski meenutada, on see, et asjatundlikkust raha eest kunagi osta ei saa. Ülikoolide diplomeid ja loomulikult ka igasuguseid ametikohti osta saab, aga reaalset haridust ning samuti haritust aga kindlasti mitte!
Teleskoobi suhteline ava, valgusjõud, fokaalsuhe ja „zargoon".
Siin tuleb jutu sisse ka arvutamist, kuid päris ilma selleta alati ka ei saa.
Oluline mõiste teleskoobi juures on suhteline ava, mis kujutab endast objektiivi läbimõõdu ja fookuskauguse jagatist ehk suhet.
Selle suuruse ruutu võtmisel saame objektiivi valgusjõu.
Kirjandusest võib kohata ka seda, et ka teleskoobi (ehk siis objektiivi) suhtelist ava nimetakse samuti mõnigi kord valgusjõuks.
„Õige" valgusjõud on tegelikult ikka suhtelise ava ruutu võetud väärtus!
Paneks tähistena ka kirja:
D/F – see on suhteline ava. D tähistab objektiivläätse läbimõõtu, F aga selle fookuskaugust.
Teleskoobiga kaasnevates dokumentides, samuti võib olla ka teleskoobi külge märgitud aga hoopis selline kirjaviis, kus täht F on jagatud mingi arvuga; kusjuures see „mingi arv" on teleskoobi fokaalsuhe FS = F/D.
Näiteks võib olla kirjas nii: F/10. See „mingi arv" (antud näitel 10) ongi siis vastava läätse fokaalsuhe.
Teleskoobi läbimõõtu (objektiivi läbimõõtu) esitatakse tihti tollides, tollides tähistamise eripära on kaks ülakoma: ''.
(Näiteks 8 tolli kirjutatakse nii: 8''.)
Ühes tollis on 2,54 cm või 25,4 mm. Objektiivi läbimõõt tollides tuleb läbi korrutada 2,54 -ga; nii saame läbimõõdu sentimeetrites. Korrutades tollid 25,4-ga, saame läbimõõdu millimeetrites.
Objektiivi läbimõõdu millimeetritesse teisendamine on sageli kasulik, sest kaasasolevatel okulaaridel on „passis" kaasa antud just millimeetrites esitatud fookuskaugused.
Meenutame nüüd taas eespool kirja pandut: okulaari läbimõõt ei võrdu teleskoobi väljundava läbimõõduga.
Teleskoobi (ja ühtlasi okulaari) väljundava läbimõõtu (mis ei ole okulaari läbimõõt!) saab arvutada mitmel moel. Üks võimalus on okulaari fookuskauguse jagamine objektiivi fokaalsuhtega. Fokaalsuhe on ühikuta suurus; seega seda arvu ümber teisendada pole vaja.
Kirjutaks selle seose ka välja: Dväljund = fokulaar / FS ,
kus FS i-ga oleme siin tähistanud selle ennist mainitud „mingi arvu".
Kordame toodud näidet, kus teleskoobi juures on esitatud selline seos: F/10; sel juhul siis FS =10.
Kui objektiivi läbimõõt D on nt 6 tolli, siis sentimeetrites on see: 15,2 cm ja millimeetrites: 152 mm.
Ka objektiivi fookuskaugus F tuleb siit kergesti kätte: F = D * FS =152 * 10 = 1520 mm = 15,2 cm = 1,52 meetrit.
Toome nüüd sisse rohkem füüsikalist mõtet. Selleks pöörame need F ja D omavahel jagamised uuesti ümber ja saame eespool juba jutuks olnud suhtelise ava. Teleskoobi suhteline ava on objektiivi fokaalsuhte pöördväärtus:
D / F = 1 / FS.
Valgusjõu saame, kui suhtelise ava ruutu võtame: (D / F)2
Ärme siis endiselt unustame, et F ja D käivad objektiivi ehk suure läätse kohta; see asub taevaobjektile lähemal; okulaar on aga vaatleja silmale lähemal.
Teleskoobi lahutusvõime ja valgusjõud on aga seda suuremad, mida suurem on objektiivi läbimõõt. Kuna fookuskauguse vähendamine vähendab omakorda ju suurendust ja seda me ka ei taha, siis jääbki üle võimalus ehitada üha suuremaid ehk siis üha suurema läbimõõduga teleskoope ja ehitatakse ka; see protsess on kestev tänapäevalgi.
Teleskoobi sisendava võime samastada objektiivi läbimõõduga. Loogiline ju, sest mida suurem objektiivi pindala, seda ulatuslikum valguskiirte kimp ehk suurem valgusvoog ka teleskoopi siseneb.
Teleskoobi okulaar, väljundava ja silmaava
Ei tohii unustada, et teleskoobi puhul on oluline ka väljundava. Mitmel korral sai juba mainitud, et kiusliku järjekindlusega võib tekkida see mõte, et väljundava võrdub teleskoobi okulaari läbimõõduga. Paraku see nii ei ole.
Okulaari asendi teleskoobis määrab asjaolu, et okulaarläätse eesmine fookus peab asuma samas kohas, kus objektiivläätse tagumine fookus. Kuna teleskoobi objektiiv on teleskoobi võimete määrajaks, on objektiiv mitmes mõttes okulaarist „suurem ja tugevam".
Seega peab objektiivi „sõna kuulama" ka okulaar oma paigutusega teleskoobis.
Nüüd aga tuleb välja, et kokkuvõttes teleskoobist väljuv valguskiirte kimp ei läbi üldjuhul kogu okulaari. Nii et teleskoobi väljundava on väiksem kui okulaari läbimõõt. Tõsi küll, alati ei pruugi see erinevus eriti suur olla. Põhimõtteliselt peab aga teadma, et erinevus on olemuslik ja sellega peab arvestama. Küllap siis just seetõttu enamasti okulaarläätsede läbimõõte sageli ei esitatagi.
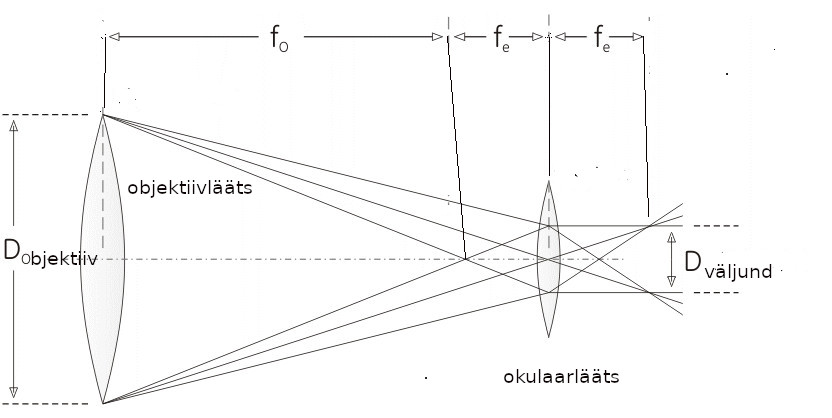
„Okulaari võimalike läbimõõtude" nime all esitatakse teleskoobil küll mõned erinevad läbimõõdud, millised okulaari torukonstruktsioonid teleskoobitoru külge sobituvad, kuid needki ei kajasta okulaarläätsede tegelikke läbimõõte ja ega meil pole neid tegelikult vajagi täpselt teada. „A ja O" on siin ikka hoopis väljundava!
Lihtsa, õhukesest läätsest okulaari juhul, on silma teleskoobivaatluseks sobivaim kaugus okulaaarist okulaari tagumise (ehk silmapoolse) fookuse kaugusel. Kuna okulaari fookuskaugus on ju üsna väike, peabki silm enam-vähem teleskoobitoru otsa juures olema (okulaar ise asub ju toru sees, silmast pisut kaugemal).
Võiks aga märkida, et teleskoopide kaasaegsed okulaarid on reeglina valmistatud keerukamate optiliste süsteemidena kui üksainus õhuke kumerlääts. Kõik ikka paremate vaatlustingimuste, ennekõike vaatevälja mõningase suurendamise huvides ehk „ühiskonna hääks" nagu ka ju vahel öeldakse. Seda arvestades võib silma parim vaatluskaugus olla veidi erinev okulaari tagumisest fookuskaugusest.
Vaatlejal võib algul tekkida vajadus ka silma asendit teleskoobi juures tasapinnaliselt „õigesti sihtida". See tähendab, et võib tekkida vajadus liigutada silma (ehk siis pead) paremale-vasakule ja/või üles-alla), et väljundavast lähtuv valguskiirte kimp ikka otse silmaläätse läbima satuks. Muidu ju lihtsalt ei paista midagi.
Valguse maksimaalse kogumise mõttes on kõige kasulikum selline okulaari valik, et teleskoobi väljundava läbimõõt võrduks (ligikaudu) silmaava läbimõõduga.
Sel juhul satub silma kogu teleskoopi läbinud valgusvoog ja uuritava objekti heledus on maksimaalne.
Tasub märkida, et teleskoobivaatlustes sobivate okulaari valikul tuleb teada, mille saavutamist vaatlusel eelistatakse. Sellise okulaari valik, millega on saavutatav vaatlusobjekti maksimaalne heledus, ei pruugi olla võrdsustatud sellise okulaari valikuga, mis tagab maksimaalse saavutatava suurenduse.
Äsja esile toodud erinevus tekib just punktikujuliseks jäävate objektide (ehk siis tähtede ja kaksik-tähtede) vaatlustel ning teisalt muude, teleskoobis punktallikatega võrreldes suuremat pinda omavate objektidena paistvate taevakehade vaatlustel. Sellised objektid on planeedid, glalaktikad, udukogud.
Silmaava läbimõõt on, olenevalt taustavalgusest ja veidi ka vaatleja vanusest, samuti mõnevõrra varieeruv, umbes 2 mm päevavalges kuni umbes 6-7 mm pimedas. Eeldades teleskoobi korral enam-vähem pimedas töötamist, võib seega arvestada silmaava suuremate väärtustega. Sageli eeldatakse maksimaalse heleduse püüdmisel optimaalse väljundava valikul just 7 mm suurust silmaava, kui silm on pimedusega täiesti harjunud.
Kui teleskoobi väljundava on silmaläätse läbimõõdust väiksem, siis väheneb ka vastavalt silmaava selle osa pindala, mis silmale valgust kogub ning ka vaadeldava pindobjekti nägemine hakkab kokkuvõttes selle tõttu nõrgenema. Teisest küljest aga (kui atmosfäär lubab) suurema kasuliku suurenduse saamine (koos detailide eristusega) veel esialgu jätkub, kui väljundava veelgi väiksemaks vähendada.
Ka maksimaalse kasuliku suurenduse osas tuleb varsti siiski alati „piir vastu". See juhtub umbkaudu siis, kui väljundava läbimõõt on 1 mm kandis. Teleskoobi suurendust veelgi suurendades hakkab objekti kujutis üha enam laiali hajuma ning tuhmuma. Olgu see objekt siis täht või planeet või mis iganes…
Kui aga teleskoobi väljundava on silmaläätsest suurem, siis osa valguskiirte kimbust silma ei satu ja heledus on omakorda selle aspekti tõttu kehvem; see kehtib just tähtedest suurema nurkläbimõõduga objektide (ehk siis punktist suurematena paistvate objektide) vaatlemisel.
Teleskoopide temaatika ei ole sellega sugugi ammendunud, edaspidi võiks seda jätkata, kuid jäägu praegu nii.
Täpselt samale järeldusele on jõudnud ka Tarmo Pihlap:
Vahemärkus
Astronoomia-tehniline jutt on vist ikkagi kuidagi pikaks kujunenud. Mis muidu ka meie kandis uudist? Keeraks õige teleka lahti?
Nüüd peaks naasma novembrikuusse ja isegi suisa enam-vähem sealse kultuurisoovituse või "kultuurisoovituse" temaatika juurde… Siit moraal: „Ära kutsu vaime välja!", nagu öeldakse…
Nõukogude miilitsa päeva eel ehk „Hommik mõrvaritega"
Saatejuht: „Uhket vikerkaare-hommikut, progressi väänatud televaatajad! On pühapäeva hommik, kuupäev parajasti 9. november. Ärme unustame, et homme, 10. novembril on Nõukogude miilitsa päev! Nagu alati, on meie saade ikka teema- ja päevakohane. Nii mõistagi ka seekord! Täna keskendume niisiis miilitsapäevale ning meie saate alateemaks on „Hommik mõrvaritega"!
Loomulikult ongi meil siin stuudios ka kaks mõrvarit: Andrus-Ahmed ja Maanus-Mohmed.
Ning muidugi on neil kaasas ka kaks nende poolt äsja mõrvatud isikut! Salam haleikum, lugupeetud kallid külalised!"
Ahmed: „Salaam!"
Mohmed: „Halaam!"
Mõistvad ja naeratavad noogutused, stuudios süveneb sume ja sõbralik õhkkond.
Saatejuht: „Esimene küsimus oleks see, mida kindlasti ka iga televaataja tahab esimesena teada: kuidas teil oma endiste nimede arabiseerimine edeneb?"
Ahmed: „Kenasti edeneb. Tulevast nädalast olen juba lihtsalt Ahmed."
Mohmed: „Ning mina olen Mohmed!"
Rahulolev naer stuudios.
Saatejuht: „No öelge asjalike ja tegusate mõrvaritena: kui suur pidu see miilitsapäev teie jaoks on?"
Ahmed: „Noh, mina pühitsen seda päeva juba nädal aega!
Mul oli siin enne tänast juba 7 pühademõrva, 1 iga päeva kohta!"
Naer stuudios.
Mohmed: „Aga minul on sinu ees 2-päevane eelis!"
Mürisev naer stuudios.
Saatejuht: „Aga kas te mäletate ka oma esimest mõrva?"
Ahmed: „Ikka mäletan. Sai siis veel maru noor oldud… Siis saigi mulle kohe ka täiesti selgeks, et see on minu kutsumus ja hobi ühekorraga!"
Mohmed: „Noh, jäi see esimene kuju mul kah juba kunagi ammu teele ette, kohe sai asi tehtud… Pärast Ahmed sooovitas ja mina ka vaatasin seda 1997. aasta Austria filmi „Naljakad mängud" ja sain samuti lõplikku kinnitust: see on minu tee".
Naerumühatus stuudios. Mõistvalt naeratav saatejuht.
Saatejuht: „Aga need, kes teil siin praegu kaasas on. Ma saan aru, et te plaanisite nad siin otse-eetris mõrvata, aga…"
Ahmed: „No nägite ise, need räpased sead tahtsid enne saate algust salaja põgenema panna!"
Mohmed: „Mis meil siis muud üle jäi…"
Saatejuht: „Ma nii muuseas küsin, et kustkohast te need siin äsja mõrvatud ka kaasa võtsite?"
„Ahmed (naerdes): "Noh, nagu ikka. Ostsime Britist, ühest sealsete moslemite peetava orjalaagi laadalt!"
„Mohmed (samuti muiates): „Lubasime kummalegi hiljem anda paar lusikatäit lisasuppi. Kohe suisa trügisid, et me nad välja valiksime!"
Ahmed: "Panime neile kohe ka mõned „toud", ikka need lollid rõõmustasid aina edasi… Nii käis asi kogu sõidu ajal."
Mohmed: „Kuni kohale jõudsime ja sa meid saatesse kutsusid. Siin nad said vist kuidagi midagi aru… Pidime tegutsema. Igavene jama, et kaamerad siis veel ei käinud."
Ahmed: „Kahju sellest ka, et stuudiopublikut pole. Võtaks sealt paar vabatahtlikku!"
Saatejuht: „Loomulikult. Arusaadav. Vabandage, publiku mittekaasamine oli tõesti minu viga. Vabatahtlikke olnuks kindlasti hulgaliselt. Kuid mis te arvate, milline on ühiskondlik kandepind teie professionaalsele huvitegevusele? Kas te vahel tunnete, et teie valitud tegevusala isegi veel inimesi ärritab?"
Mohmed: „Ei tunneta küll. Tundub, et Eesti on oma arenguga jõudnud Lääne kultuuriruumile piisavalt lähedale."
Ahmed: „Selles osas on jah asi korras. Inimesed ei imesta enam ammu millegi üle!"
Mohmed: „Keegi isegi ei vaata imelikult. Tajume vaid sõbralikke pilke."
Ahmed: „Sageli inimesed astuvad ise ligi ja tunnustavad."
Ka Saatejuht noogutab taas kord ja sealjuures mõistagi ka tunnustavalt.
Saatejuht: „Aga kas teil on ka plaanid oma tegevust kuidagi laiendada ja arendada?"
Ahmed: „Muidugi. Me Mohmediga ja teiste sõpradega peame plaani avada mõrvarite kursused. Kaugem perspektiiv on Mõrvaakadeemia rajamine."
Mohmed: „ Mõrvakonveier käigu nagu vahetused palliplatsil. Vahetusmeeste pink peab tihedasti täidetud olema!"
Ahmed: „Keegi peab ju edaspidi ka meie töö üle võtma."
Mohmed: „Küll on siis hea, piip hambus, vaadata, kuidas uus generatsioon töötab!"
Muhe naer stuudios.
Saatejuht: „Eks meilgi ole omi arenguplaane. Aastavahetuseks on plaanis suurepärane kogupere otse-eetri telemäng: „Kes tapab rohkem?" On uhke tõdeda, et stuudio-mõrvarite konkurss on juba välja kuulutatud ja konkurss on ÄÄRMISELT tihe! Teie mõlemad olete vana tutvuse poolest muidugi juba ilma konkursita välja valitud! Ning ka mõrvatavate konkurss on avatud ning, uskuge mind, see on peaaegu sama tihe!"
Ahmed: „Seda aastavahetust tasub oodata!"
Mohmed: „Tasub! Märksa rohkem kui eelmist!"
Saatejuht: „Loomulikult!"
Kokkuvõttev ja vastastikku mõistev paus.
Saatejuht: „Meeldiv oli näha teid saates osalemas, Andrus ja Maanus!"
Ahmed ja Mohmed: „MIS??? MIS SA ÜTLESID!!!"
Jubedasti ehmunud saatejuht, kes enda lemmikutest mõrvarite esialgsete ehk õigete nimede väljaütlemisega kogemata vääratas, põgeneb kabuhirmus, vihased retsidivistid-mõrvarid nugadega kannul. Paraku ei tunne need eriti stuudio sisustust, mõlemad komistavad stuudio nööride otsa ning mõrvavad kogemata hoopis iseendid.
Nüüd on stuudios kokku juba 4 mõrvatud. Saatejuht on kadunud.
Pea pistab stuudiosse nutune AL Bundy: „Krt, hiljaks jäin jälle. Tahtsin ju ennast neile tapjaile vabatahtlikuks pakkuda… 10 tuhhi jäi jälle saamata!"
Kultuuriminister on kogu saadet ohutust, kõige kaugemast ja pimedamast lukustamata välisuksega ühendatud nurgast („täiesti juhuslikult" seisab sama ukse taga töötava mootoriga ja lahtise uksega auto koos stardivalmis autojuhiga), õnnest üleni säravana jälginud. Nüüd korraga, samuti juba kurvana, on ka Kultuuriminister avalikult kohal ja lohutab AL-i: „Vastavalt seadusele mina siin sekkuda ei saa!"
Needki kaks liberaalset, kuid see-eest (sarnaselt saatejuhile ja oi kui mitmetele teistele) põhiliselt vaid spinaalset mõistust omavat kurba õnnetushunnikut hakkavad lõpuks samuti stuudiost ära minema. Koperdavad aga nemadki lavatehnika otsa ja katsetavad, kas Maa külgetõmme ka nende peal ikka parajasti toimib. Toimib küll! Nende endi õnneks pole aga neil vähemalt peos lahti olevaid relvi kaasas…
Ka on Saatejuhiga vähemalt väliselt ikka kõik hästi. Sest juba nädal hiljem tuleb televaatajail teda taas välja kannatama hakata.
Nagu kogu seda hälvikute organisatsiooni.
Ega ikka ei kannata küll!
Kultuurisoovitus püüab kujunenud musta meeleolu veidi vähem süngeks muuta, kuigi temaatika eelnevast palju erinev polegi. Vähemalt esineb mingeid pürgimusi normaalsema tuleviku suunas… Lugu ise on „Morgani kohtumine Organitega".
Tänasel päeval tekib seda lugu vaadates/kuulates ka mõnigi täiendav mõte võrreldes 1989. aastaga…
Loo esmakordne esitus oli nimelt 1989. aasta vana-aasta õhtul. Isikliku ja muidugi subjektiivse mälu järgi oli sel õhtul üldse üks aegade parimaid aastalõpu teleprogramme. Mõstagi ei olnud siis veel tegu mingi „err"-iga, vaatamata eksitavale logole.
